The value of a future promise to pay or receive a single amount at a specified interest rate is called the present value of a single amount. Many times in business and life, we want to determine the value today of receiving a specific single amount at some time in the future. For example, suppose you want to know the value today of receiving $15,000 at the end of 5 years if a rate of return of 12% is earned. Another way of asking this question is: What amount would you need to invest today at 12% compounded annually in order to receive $15,000 after 5 years? Problems and questions like this are known as "present value of a single amount problems." This is because we are interested in finding the present value, or the value today, of receiving a set sum in the future. Intuitively, we know that the present value will be less than the future value. For example, if you had the choice of receiving $12,000 today or in 2 years, you would take the $12,000 today. This is because you can invest the $12,000 so that it will accumulate to more than $12,000 at the end of 2 years. Another way of looking at this is to say that because of the time value of money, you would take an amount less than $12,000 if you could receive it today, instead of $12,000 in 2years. The amount you would be willing to accept depends on the interest rate or the rate of return you receive. The formula used to calculate the present value of a single amount is: In this formula, the following variables are defined as: Suppose a company expects to receive $8,000 after 5 years. Calculate the present value of this sum if the current market interest rate is 12% and the interest is compounded annually. The way to solve this is to apply the above present value formula. In this example, the number of periods (n) is 5 and the interest rate (i) is 12%. Therefore, the present value (PV) is calculated as follows: PV = FV x 1 / (1+i)n = 8,000 x 1 / (1+12%)5 = 8,000 x 1 / (1+0.12)5 = 8,000 x 1 / (1.12)5 = 8,000 x 1 / 1.7623 = 8,000 x 0.5674 = $4,540 According to these results, the amount of $8,000, which will be received after 5 years, has a present value of $4,540. This example shows that if the $4,540 is invested today at 12% interest per year, compounded annually, it will grow to $8,000 after 5 years. In present value situations, the interest rate is often called the discount rate. This is because we are discounting a future value back to the present. Some individuals refer to present value problems as "discounted present value problems." One way to solve present value problems is to apply the general formula we developed for the future value of a single amount problems. For example, returning to the previous example, assume that at the end of 5 years, you aim to have $15,000. If you can earn 12% interest compounded annually, how much do you need to invest today? Using the general formula for the present value table, the answer is $8,511.40. The working is as follows: Accumulated amount = Factor x Principal Principal = Accumulated amount / Factor = $15,000 / 1.7623 = $8,511.40 This is equivalent to saying that at a 12% interest rate compounded annually, it does not matter whether you receive $8,511.40 today or $15,000 at the end of 5 years. Based on this result, if someone offered you an investment at a cost of $8,000 that would return $15,000 at the end of 5 years, you would do well to take it if the minimum rate of return was 12%. This is because at 12% the $15,000 is actually worth $8,511.45 today, but you would need to make an outlay of only $8,000. Rather than using future value tables and making adjustments to the general formula, it is possible to use present value tables. Similar to future value tables, present value tables are based on the mathematical formula used to determine present value. Due to the relationship between future and present values, the present value table is the inverse of the future value table. The example below is an excerpt from a present value table. The table works the same way as a future value table, with the exception that the general formula is: Present value = Factor x Accumulated amount For example, if we want to use the table to determine the present value of $15,000 to be received at the end of 5 years (compounded annually at 12%), we simply look down the 12% column and multiply that factor by $15,000. So, the answer is $8,511.45. This is determined as follows: Present value = Factor x Accumulated amount = 0.56743 x $15,000 = $8,511.45 As shown in the future value case, the general formula is useful for solving other variations as long as we know two of the three variables. For example, suppose you want to know what interest rate (compounded semi-annually) you need to earn in order to accumulate $10,000 at the end of 3 years, with an investment of $7,049.60 today. The answer is 6% semi-annually (or 12% annually), which is determined follows: Present value = Factor x Accumulated amount Factor = Present value / Accumulated amount = $7,049.60 / $10,000.00 = 0.70496 Looking across the sixth row in the present value table shown above, we arrive at a value of 0.70496 where it meets the 6% column. Given that interest is compounded semi-annually, the annual rate is 12%. When you start working with time value of money problems, you need to pay attention to distinguish between present value and future value problems. One way to achieve this is to use timelines to analyze the situation. For example, a timeline is shown below for the example above, where we calculated the future value of $10,000 compounded at 12% for 3 years. Also, a timeline for the present value of $15,000 (discounted back at 12% for 5 years) is given as follows:What Is the Present Value of a Single Amount?
Present Value of a Single Amount: Explanation
Formula For Present Value of a Single Amount
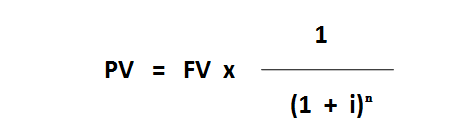
Example
Solution
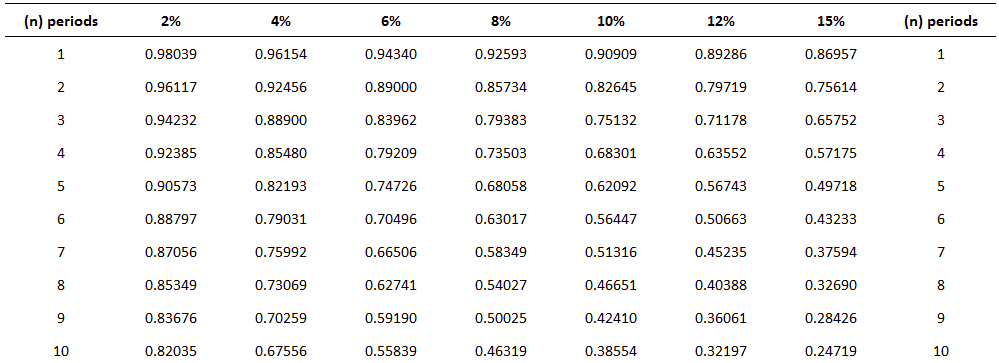
Using Present Value Tables
Other Present Value Situations
Distinguishing Between the Future Value and Present Value of a Single Amount
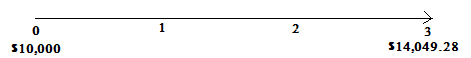

Present Value of a Single Amount FAQs
The present value of a single amount is an investment that will be worth a specific sum in the future. For example, if you invest $1,000 today at an interest rate of 12%, it'll be worth $2,000 in 5 years.
To solve the problem presented above, first, determine the future value of $1,000 invested at 12%. Then, divide that number by 1 plus your desired interest rate. So, in this case, you'd divide $2,000 by (1 + 0.12), Which is 2.24%.
The present value of a single amount formula is most often used to determine whether or not an investment opportunity is good.
As shown above, the future value of an investment can be found by using the present value of a single amount formula and adjusting for compound interest.
One way to tell if you're looking at a future value or present value problem is to look at how many times the interest rate is being applied. In the future value example illustrated above, the interest rate was applied once because the investment was compounded annually. In the present value example, however, the interest rate is applied twice. This means that the future value problem involves compounding while present value problems involve discounting.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.













