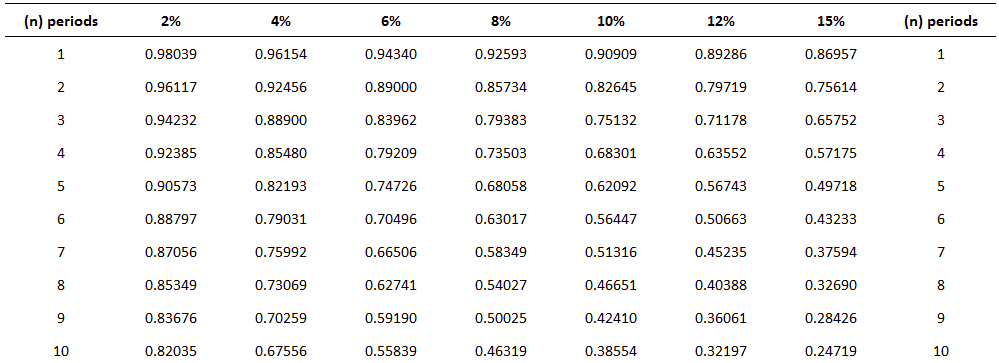
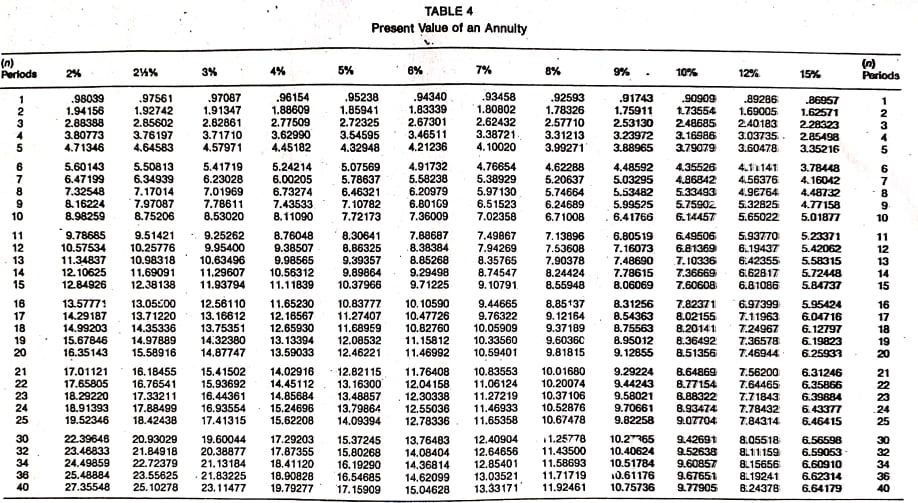
The present value of an annuity refers to the present value of a series of future promises to pay or receive an annuity at a specified interest rate. The value today of a series of equal payments or receipts to be made or received on specified future dates is called the present value of an annuity. As with the future value of an annuity, the receipts or payments are made in the future. Present value is the value today, where future value relates to accumulated future value. The present value of a series of payments or receipts will be less than the total of the same payment or receipts. This is because cash received in the future is not as valuable as cash received today. On the other hand, the future value of an annuity will be greater than the sum of the individual payments or receipts because interest is accumulated on the payments. It is important to distinguish between the future value and the present value of an annuity. Again, timelines are helpful in this respect. Mortgages and certain notes payable in equal installments are examples of present-value-of-annuity problems. For example, suppose that a bank lends you $60,000 today, which is to be repaid in equal monthly installments over 30 years. In this case, the bank will want to know what series of monthly payments, when discounted back at the agreed-upon interest rate, is equal to the present value today of the amount of the loan. Suppose you want to determine the value today of receiving $1.00 at the end of each of the next 4 years. The appropriate interest or discount rate is 12%. To solve this, we can construct a table that determines the present values of each of the receipts. Thus, the present value of receiving the four $1.00 payments is $3.03735 when discounted at 12%. Each of the individual dollars was discounted using the factors in the present value of a single amount table (see below). For example, the present value of the dollar received at the end of year 4, when discounted back 4 years, is $0.63552. It must be discounted back 4 years because the present, or today, is the beginning of year 1. The dollar received at the end of year 3 must be discounted back 3 periods; the dollar received at the end of year 2 must be discounted back 2 periods; and so forth. As with the calculation of the future value of an annuity, we can use prepared tables. The following table is an example of such a table. This table is constructed by summing the individual present values of $1.00 at set interest rates and periods. Thus, the factor for the present value of four amounts of $1 .00—to be received at the end of each of the next 4 years when discounted back at 12%—is 3.03735 (the value we determined independently above). Problems involving the present value of an annuity are solved using the following general formula: Present value of an annuity = Factor x Amount of the annuity As long as we know two of the three variables, we can solve for the third. Thus, we can determine the present value of the annuity, interest rate, number of periods, or amount of the annuity. To demonstrate how to calculate the present value of an annuity, assume that you are offered an investment that pays $2,000 a year at the end of each of the next 10 years. How much would you pay for the investment if you wanted to earn a rate of return of 8%? This is a present-value problem because you would pay the value today of this stream of payments discounted back at 8%. This amount is $13,420.16, determined as follows: Present value of an annuity = Factor x Amount of the annuity = 6.71008 x $2,000 = $13,420.16 Another way to interpret this problem is to say that, if you want to earn 8%, it makes no difference whether you keep $13,420.16 today or receive $2,000 a year for 10 years. A common variation of present value problems involves calculating the annuity payment. In many cases, these are loan or mortgage problems. For example, assume that you purchase a house for $100,000 and make a 20% down payment. You intend to borrow the rest of the money from the bank at 10% interest. To make the problem easier, suppose that you will make 30 yearly payments at the end of each of the next 30 years. What will your yearly payments be? In this case, you need to borrow $80,000 ($100,000 x 80%). Therefore, the yearly payment would be $8,486.34, determined as follows: Present value of an annuity = Factor x Amount of the annuity Amount of the annuity = Present value of an annuity / Factor = $80,000 / 9.42691 = $8,486.34 Suppose that Black Lighting Co. purchased a new printing press for $100,000. The quarterly payments are $4,326.24 and the rate is 12% annually (or 3% per quarter). How many payments are needed to pay off the loan? In this case, 40 payments are required. This is determined as follows: Present value of an annuity = Factor x Amount of the annuity Factor = Present value of an annuity / Amount of the annuity = $100,000 / $4,326.24 = 23.11477 Looking down the 3% column in Table 2 we find the factor 23.11477 at the fortieth-period row. Thus, 40 quarterly payments are needed to pay off the loan. Many accounting applications related to the time value of money involve both single amounts and annuities. For example, suppose that you are considering purchasing an apartment. After much deliberation, you determine that you will receive net yearly cash flows of $10,000 from rental revenue, less rental expenses from the apartment. To make the analysis easier, let's assume that the cash flows are generated at the end of each year. These cash flows will continue for 20 years, at which time you estimate that you can sell the apartment building for $250,000. How much should you pay for the building, assuming that you want to earn a rate of return of 10%? This problem involves an annuity (the yearly net cash flows of $10,000) and a single amount (the $250,000 to be received once at the end of the twentieth year). As a rational person, the maximum that you would be willing to pay is the value today of these two cash flows discounted at 10%. That value is $122,296, as determined below.Present Value of an Annuity: Definition
Present Value of an Annuity: Explanation
Determining the Present Value of an Annuity
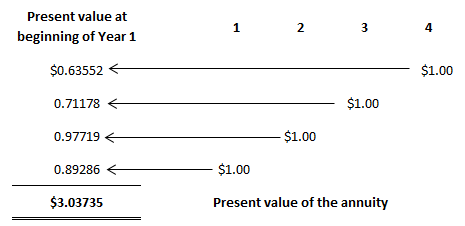
Problems Involving the Present Value of an Annuity
Determining the Present Value
Determining the Annuity Payment
Determining the Number of Payments
Combination Problems
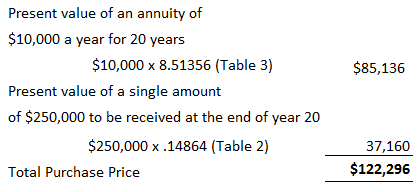
Present Value of an Annuity FAQs
The present value of annuity is the current worth or cost of a fixed stream of future payments. This may be found by discounting each cash flow back at a given rate. This can be calculated using various financial tools, including tables and calculators, which are available on the web or in books of tables.
The term “present value” refers to an individual cash flow at one point in time, whereas the term “annuity” is used more generally to refer to a series of cash flows. The present value of an annuity is a calculation used to determine the current worth or cost of a fixed stream of future payments. In contrast, the annuity factor is used to calculate how much money must be invested at a given rate of return over a certain period for it to accumulate to a specific sum in the future.
The present value of annuity table contains the factors used to determine an individual cash flow at one point in time. This can be done by discounting each cash flow back at a given rate by using various financial tools, including tables and calculators.
To determine an individual cash flow, or annuity factor, by using this table, you would look across the top row for the number of periods and down the left side for the interest (or discount) rate. Entering these values in an equation yields the present value of an annuity.
An individual cash flow or annuity can be determined by discounting each cash flow back at a given rate using various financial tools, including tables and calculators. The "present value" term refers to an individual cash flow at one point in time, while the term "annuity" is used more generally to refer to a series of cash flows.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.













