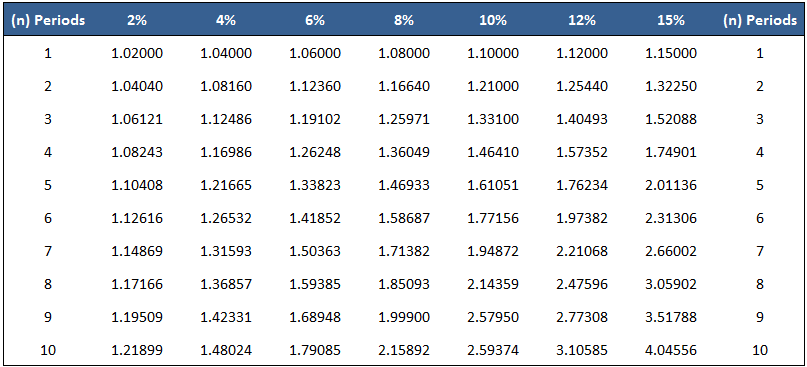
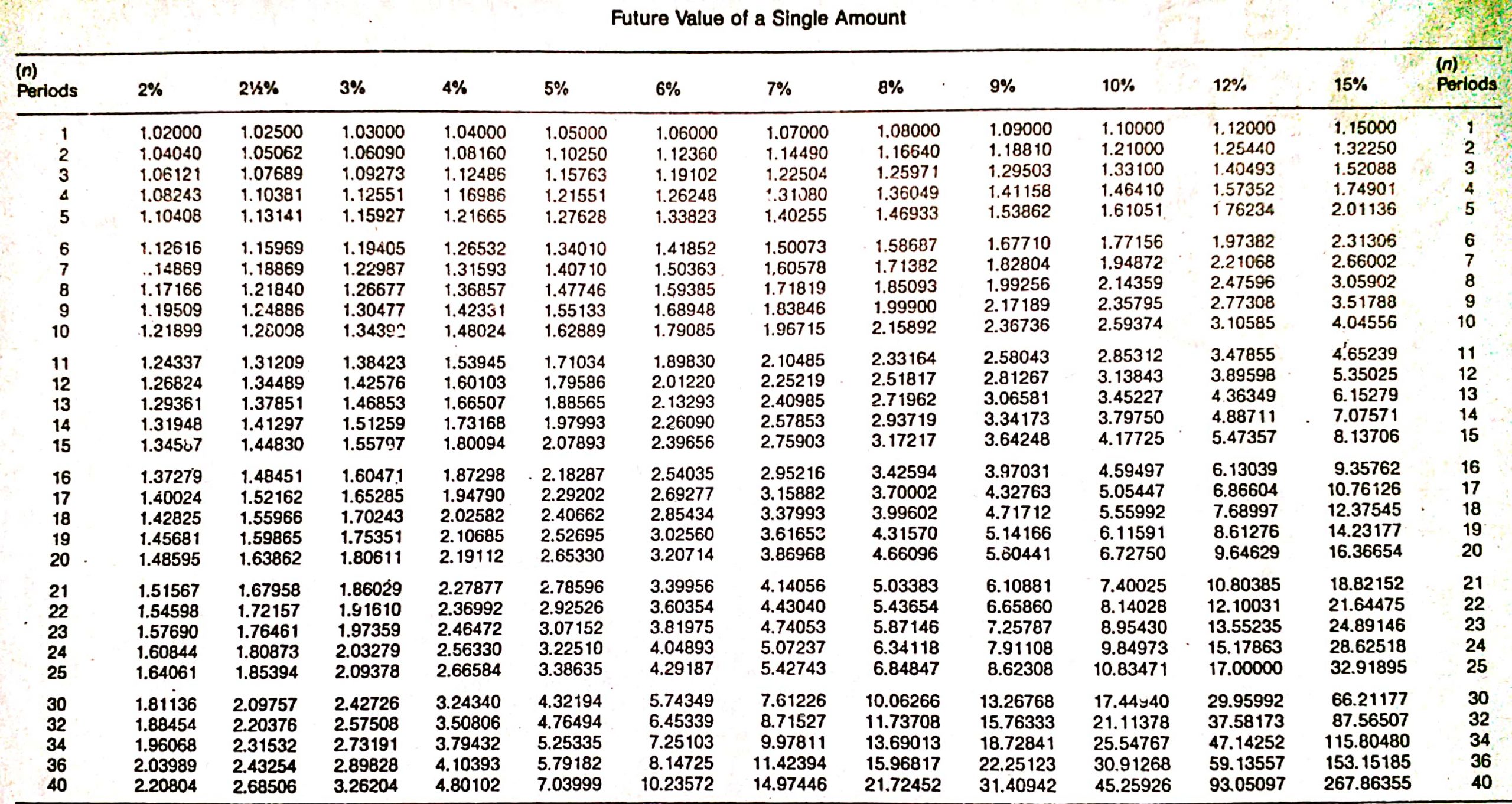
The value of a current single amount taken to a future date at a specified interest rate is called the future value of a single amount. In this case, "future value" means the amount to which the investment will grow at a future date if interest is compounded. The single amount refers to a lump sum invested at the beginning of a period (e.g., year 1) and left intact for all periods. To explain the concept of the future value of a single amount, let's start with the table below. In this table, we see what the future amount of $10,000 invested at 12% annual interest for three years would be, given a certain compounding pattern. This is an example of determining the future value of a single amount. There were no additional investments or interest withdrawals. These future value or compound interest calculations are important in many personal and business financial decisions. Suppose a company is interested in determining the worth of a $50,000 investment after 5 years if interest is compounded semi-annually versus quarterly, or what rate of return must be earned on a $10,000 investment if $18,000 is needed in 7 years. Both situations are problems where the solution is to determine the future value of a single amount. One way to solve problems of this type is to construct tables similar to the one shown above. However, this method is time-consuming and not very flexible. Mathematical formulas can also be used. For example, the tables used above to determine the accumulated amount of a single amount at different compounded rates are based on the formula described in the next section. In this formula, the variables are defined as follows: In the example of the amount of $10,000 compounded annually for 3 years at 12%, the $14,049.28 can be determined by the following calculation: = $10,000(1 + .12)3 = $14,049.28 However, one of the simplest methods is to use tables that give the future value of $1 at different interest rates and for different periods. Essentially, these tables interpret the above mathematical formula for various interest rates and compounding periods for a principal amount of $1. Once the amount for $1 is known, it is easy to determine the amount for any principal by multiplying the future amount for $1 by the required principal amount. Many hand calculators also have function keys that can be used to solve these types of problems. To illustrate, the table below shows the future value of $1 for 10 periods with interest rates ranging from 2% to 15%. Continuing with the same example, suppose we now want to determine the future value of $10,000 at the end of 3 years if interest is compounded annually at 12%. To solve this, we can check the 12% column in the table until we come to 3 interest periods. The factor from the table is 1.40493, which means that $1 invested today at 12% will accumulate to $1.405 at the end of 3 years. Because we are interested in $10,000 rather than $1, we just multiply the factor of 1.40493 by $10,000 to determine the future value of the principal amount. The amount is $14,049.30, which, except for a slight rounding error, is the same as we found in the table. We can generalize the use of the future value table with the following formula: Accumulated amount = Factor (from the table) x Principal = 1.40493 x $10,000 = $14,049.30 This formula can be used to solve a variety of related problems. For example, as we noted above, you may be interested in determining what rate of interest must be earned on a $10,000 investment if you want to accumulate $18,000 at the end of 7 years. Or you may want to know the number of years an amount must be invested in order to grow to a certain amount. In all these cases, we have two of the three items in the formula, and we can solve for the third. Interest is usually compounded more often than once per year. In these situations, we simply adjust the number of interest periods and the interest rate. For example, to work out what $10,000 will be worth after 3 years if interest is compounded quarterly at an annual rate of 12%, we simply check the 3% column until we reach 12 periods (see Table 1.1). Table 1.1 The factor is 1.42576. Using the general formula, the accumulated amount is $14,257.60, which is determined as follows: Accumulated amount = Factor x Principal = 1.42576 x $10,000 = $14,257.60 There are many situations in which the unknown variable is the number of interest periods that the dollars must remain invested or the rate of return (interest rate) that must be earned. For example, assume that you invest $5,000 today in a savings and loan association that will pay interest compounded annually. You need to accumulate $8,857.80 for a certain project. How many years does the investment have to remain in the savings and loan association? Using the general formula, we can tell that the answer is 6 years, which is calculated as follows: Accumulated amount = Factor x Principal Factor = Accumulated amount / Principal = $8,857.80 / $5,000.00 = 1.77156 Looking down the 10% column in Table 1.1, the factor of 1.77156 appears at the sixth-period row. Given that interest is compounded annually, the sixth period is interpreted as 6 years. This example was constructed so that the factor equals a round number of periods. If it does not, interpolation is needed. The examples, exercises, and problems in this article do not require interpolation. We can use the same method to determine the required interest rate. For example, suppose that you invest $10,000 for 8 years. What rate of return or interest rate, compounded annually, must you earn if you want to accumulate $30,590.23? Using the general formula, we can work out that the answer is 15%. This is determined as follows: Accumulated amount = Factor x Principal Factor = Accumulated amount / Principal = $30,590.23 / $10,000.00 = 3.05902 Looking across the eighth-period row, we find the factor of 3.05902 at the 15% column.What Is the Future Value of a Single Amount?
Explanation

Example
Formula for Accumulated Amount at Different Compounded Rates

Interest Compounded More Often Than Annually
Determining the Number of Periods or the Interest Rate
Future Value of a Single Amount FAQs
The future value is the total amount received at a given date when that amount includes an initial investment plus all interest earned from the initial investment.
The calculation of the future value is used for many different accounting functions. The most common use is to understand how much money will be received at a given date because of interest earned on an investment. For example, if you invest $5,000 today in a savings account that pays 2% interest each year compounded annually, then you can calculate the future value of this amount as a projected Cash Flow.
Future value = p x (1+i)n where: p = principal; initial investment i = interest rate that compounds n times per year n = the number of times that interest is compounded per year.
The calculation of the future value allows you to project the total amount that will be available at some date in the future based on specified assumptions. Future value calculations allow investors and managers to determine how much interest they can earn on their money.
The future value calculation is often used to determine projected Cash Flows. This calculation does not include consideration of any additional investments that may be needed for tax or other reasons. It also assumes that the interest rate will remain constant throughout the life of the investment, which is almost never true in practice.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.













